Uncertainty in Measurement
There are two kinds of numerical data: exact and inexact. Exact data are numbers that are known exactly. Inexact data are numbers that are not known and have a degree of uncertainty. When experiments are carried out, there will always be a degree of uncertainty. Uncertainty of measurement is the doubt that exists about the result of a measurement. There is always a margin of error for any instrument. Usually, the margin of error is expressed as +/-, which provides a range that the actual measurement falls within.
Laboratory glassware usually lists the uncertainty directly on the instrument. But just in case, the uncertainty of analog instruments (such as graduated cylinders & burets) is +/- half of the smallest division. The uncertainty of digital instruments (electronic balances, timers & thermometers) is +/- the smallest scale division.
Example: A stick that is 30 centimeters with an uncertainty of +/- 1cm means that the stick is actually between 29 and 31 centimeters long. Most electronic balances read to 0.01g, but others (ones used in precise analytical experimentation) read to 0.0001 or better.
Human error can also factor into uncertainty.
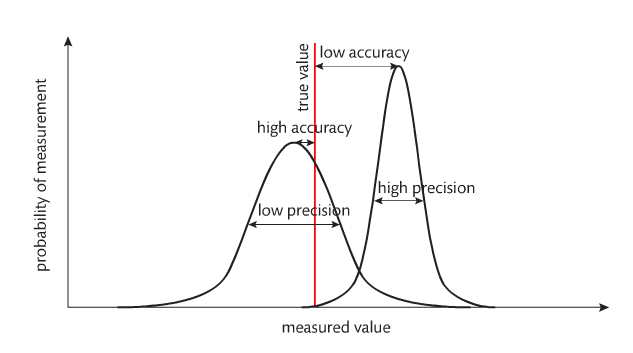
Accuracy refers to how close a measurement is to the accepted (correct) value. Precision refers to how close (or consistent) measurements are to one another. Accuracy refers to one measurement. Precision refers to multiple measurements. For example, look at the following images:
Bullseye 1
Bullseye 2
To determine the accuracy of an experiment, percent error is used. The formula for percent error is:
PE = |(accepted-experimental) / accepted| * 100
Accepted values are known; experimental values have been calculated in laboratory.
Precision is determined via the use of significant figures.
Laboratory glassware usually lists the uncertainty directly on the instrument. But just in case, the uncertainty of analog instruments (such as graduated cylinders & burets) is +/- half of the smallest division. The uncertainty of digital instruments (electronic balances, timers & thermometers) is +/- the smallest scale division.
Example: A stick that is 30 centimeters with an uncertainty of +/- 1cm means that the stick is actually between 29 and 31 centimeters long. Most electronic balances read to 0.01g, but others (ones used in precise analytical experimentation) read to 0.0001 or better.
Human error can also factor into uncertainty.
Accuracy refers to how close a measurement is to the accepted (correct) value. Precision refers to how close (or consistent) measurements are to one another. Accuracy refers to one measurement. Precision refers to multiple measurements. For example, look at the following images:
Bullseye 1
Bullseye 2
To determine the accuracy of an experiment, percent error is used. The formula for percent error is:
PE = |(accepted-experimental) / accepted| * 100
Accepted values are known; experimental values have been calculated in laboratory.
Precision is determined via the use of significant figures.
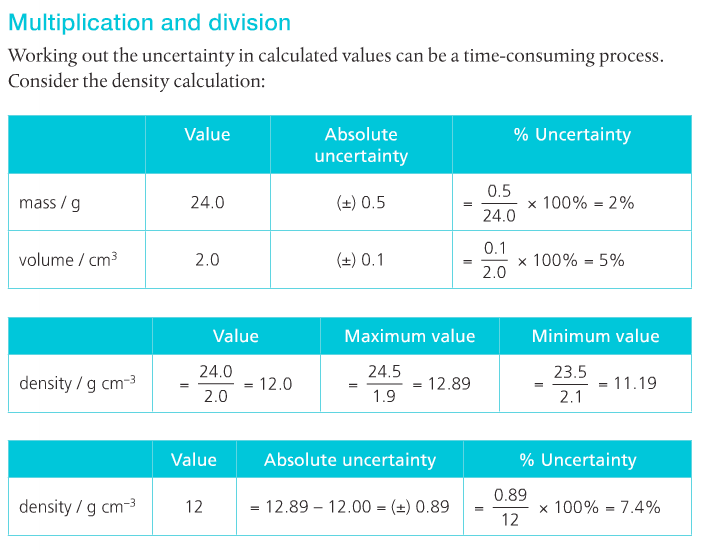
Absolute uncertainty (delta A) is the margin of uncertainty associated with the result from a given measurement. Relative uncertainty (A) is the ratio comparing the size of the absolute uncertainty to the size of the measured experimental result.
Uncertainties in raw data lead to uncertainties in processed data. This must be considered.
Uncertainties in raw data lead to uncertainties in processed data. This must be considered.
Significant Figures
Significant figures refers to the number of digits reflecting the precision of a given measurement. The greater the number of SF, the greater the certainty about the numerical value of the measured or calculated quantity.
For operations involving multiplication or division: The result should be expressed based on the measurement with the smallest number of sig figs.
For operations involving addition or subtraction: The result should be expressed based on the measurement with the smallest number of decimal places.
For operations involving multiplication or division: The result should be expressed based on the measurement with the smallest number of sig figs.
For operations involving addition or subtraction: The result should be expressed based on the measurement with the smallest number of decimal places.
Experimental Error
Experimental error is the difference between the recorded value and the generally accepted value. Errors can be systematic or random. Systematic errors occur as a result of poor experimental design or procedure. An example of systematic error is reading the meniscus in a graduated cylinder incorrectly, using too much liquid in titration, and incorrectly zeroing an electronic balance. The only way systematic errors can be reduced is by careful experimental design.
Random errors are caused by the readability of an instrument, environmental changes and effects (such as room temperature), insufficient data, and human error. Random error can be reduced by experiment replication or repeatability.
NOTE: Don't confuse error and uncertainty. Error is the difference between obtained results and the actual accepted value. Uncertainty is the doubt regarding the measurement obtained.
Random errors are caused by the readability of an instrument, environmental changes and effects (such as room temperature), insufficient data, and human error. Random error can be reduced by experiment replication or repeatability.
NOTE: Don't confuse error and uncertainty. Error is the difference between obtained results and the actual accepted value. Uncertainty is the doubt regarding the measurement obtained.